一步一步教你怎样解魔方
支付宝内搜索 9155838 即可领现金红包 每天都能领哦
一般人肯定玩过魔方吧，转出来了吗？其实解魔方的方法有很多种，最近集众家之所长摸索出一种傻瓜解法，很好上手，不过也有公式要背。
首先介绍一下基础的东西：
国际通用的算法是美国魔方大师辛马斯特创造的。
魔方有6个面，他是这样定义：
F = front face =前面 ；B = back face =后面
R = right face =右面； L = left face =左面 ；
U = up face =上面 ； D = down face =下面
F代表前面顺时针转一次，F'代表前面逆时针转一次，R2代表右面转二次。
（而世界上大多数魔方高手使用的方法是被称为“Fridrich Method”的复原法，这种方法是由美国人Jessica Fridrich女士发明的。大家可以研究一下）
开始了，先选一个你喜欢的颜色。下面以蓝面为例。
第一步：在第一面做一个十字。注意，每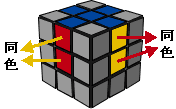
个侧面的棱和中心是同色的。即
（ 图中灰色块就是不需注意块）
。很简单，相信你能独立搞定。
第二步）对好顶面，并在四侧面成T字。即
。
解法如下：你会发现蓝色角块就6种位置
。
对于A位置，只3步：F D F’。（罗嗦一下，F即把红面顺时针转动一次。。。。。）
对于B位置， 需3步：R’D’R。
对于其它位置，你总可以用旋转侧面和底面将其转到A或B。（超简单，如果我把公式写出来，你会觉得侮辱了你的智商。）
第三步）完成第二层，变成形如
。就是把顶面每边中间的色块复原。
情况一： 
公式： U R U’R’ U’F’U F
结果：把红白色块复原。（箭头所指处）。
情况二： 
公式： U’F’U F U R U’R’
结果：把红白色块复原。（箭头所指处）。
注意：会有一些情况下，你需要的棱色块不在顶面，而在第二层。
首先，你要先做在顶面上的那些， 可能不听话的棱色块会自己变到顶面上，如果最后他还是不听话，我们只有灵活运用上两个公式，把它搞到顶面。
第四步）在魔方新的顶面上成十字。形成
。
解法：把魔方翻过来，绿面朝上。此时，你的魔方只有4种情况：
1
2
3
还有一种是已经完成。（不要管其它色块）。
本人认为只需掌握一个公式 R’U’F’U F R。
反复用它，直到成功。（注意：转动之前请把魔方按图中位置对好）。
第五步）翻转魔方顶面四角，对好顶面颜色，使之形成 
。
你的魔方只会有8种情况：
还有一种是已经完成。（图太大了，可以图片另存为后 再看）
（注意：转动之前请把魔方按图中位置对好）。
对于情况1，公式：R’U’R U’R’U2 R。
对于情况2， 公式：F U F’U F U2 F’。
对于其它情况，你可灵活用上两个公式，它会变到情况1或情况2。
现在是不是很激动。还有两步就完全搞定了。
第六步）调整四角顺序，完成顶面。使之形成：
。
你有1/6的概率已经完成。如果不是，就首先找一条边，这条边的两个角有相同的颜色（概率2/3）。两角中间的棱颜色和下面两层的颜色我们不用关心。现在把这条边放在背面，
公式：L F’ L B2 L’ F L B2 L2
如果你找不到这样一条有两角同色的边，你就闭着眼睛应用一遍上面的算法，就一定可以找到。
第七步）将最后的棱色块顺序排列好。观察你的魔方，你可能需要以下变换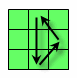
。
公式R2 U' F B' R2 F R2' B U'。我们称为顺时针公式
或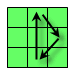
R2 U F B' R2 F' B U R2 逆时针公式
（再罗嗦一下，Ｂ就是把背面对着自己，顺时针转动一次）
如果你需要作如下两个变换
。你随便应用一遍上面顺时针或逆时针的算法，然后他就会变成顺时针或逆时针的情况了。
成功! 基本上睁着眼睛两个小时可完成。
提高解魔方成绩的瓶颈在于:
1,魔方的质量,好的魔方很滑的;
2,公式的熟练程度;
3,记的公式的多少;
4,解题方法的突破.
更新于:2009-02-06 21:21:43 栏目:生活日记 关键词:魔方
本站使用「署名 4.0 国际」创作共享协议，可转载、引用，但需署名作者且注明文章出处
你试过吗?
真得可行?